Type-Safe Tensor Operations

A deep dive into how torch.js catches shape errors at compile time using TypeScript’s type system.

Table of Contents

  1. Introduction: What Are We Building?
  2. Glossary: Math Terms You’ll Need
  3. Part 1: What is a Tensor?
  4. Part 2: The Shape Problem
  5. Part 3: TypeScript Types 101
  6. Part 4: Building Blocks - Type-Level Arithmetic
  7. Part 5: Branded Error Types
  8. Part 6: Einsum - Parsing Math Notation
  9. Part 7: Einops - A Better Pattern Language
  10. Part 8: Practical Slicing with .at()
  11. Part 9: Testing Type-Level Code
  12. Part 10: Tensor Expressions - Parsing Math at the Type Level
  13. Part 11: Putting It All Together
  14. Conclusion

Introduction: What Are We Building?

Introduction to type-safe tensor operations

Imagine you’re building a machine learning model. You have some data, you multiply matrices, reshape arrays, and combine things in complex ways. Then you run your code and... crash.

RuntimeError: mat1 and mat2 shapes cannot be multiplied (2x3 and 5x4)

You stare at the error. Which line caused this? You add print statements everywhere. You trace through the code. Twenty minutes later, you find the bug: you passed the wrong tensor to a function.

What if your code editor could catch this mistake before you even ran the code?

That’s what we built in torch.js. When you write:

const a = torch.zeros(2, 3);  // A 2x3 matrix of zeros
const b = torch.zeros(5, 4);  // A 5x4 matrix of zeros
const c = a.matmul(b);        // Matrix multiplication

Your editor immediately shows a red squiggle under a.matmul(b) with the message:

Type 'matmul_error_inner_dimensions_do_not_match<3, 5, [2,3], [5,4]>'
is not assignable to type 'Tensor'

The error tells you exactly what’s wrong: you tried to multiply a matrix with 3 columns by a matrix with 5 rows, but those numbers need to match.

This article will teach you how we built this. We’ll start from the very basics - what a tensor even is - and build up to parsing complex mathematical notation entirely within TypeScript’s type system.

By the end, you’ll understand:

  • How TypeScript’s types can do computation, not just validation
  • How to parse strings at compile time
  • How to build type-safe domain-specific languages
  • Patterns you can use in your own projects

Not a machine learning developer? That’s fine - tensors are just our example domain. The techniques in this article are the same ones powering tRPC’s type-safe APIs, Prisma’s typed queries, Zod’s schema inference, Hono’s route parameters, and more. By the end, you’ll be able to build your own type-safe DSLs for forms, configs, APIs, or anything else.

Let’s dive in!

TypeScript’s Secret Superpower

But first, here’s something surprising: TypeScript’s type system can compute.

Most type systems just label values - this is a string, that’s a number. But TypeScript’s can do much more:

What
Parse strings
How
Template literal types
Example
SplitArrow<'ij->jk'> -> { inputs: 'ij', output: 'jk' }
What
Add numbers
How
Tuple length tricks
Example
Add<2, 3> -> 5
What
Validate shapes
How
Conditional types
Example
matmul([2,3], [5,4]) -> compile error!

This means we can catch tensor shape errors before your code even runs. No runtime cost - all the checking happens during compilation.

We’ll build all of this step by step, starting with the simplest idea: using tuple lengths to represent numbers.

Glossary: Math Terms You’ll Need

Before we start, here’s a quick reference for mathematical terms we’ll use. Don’t worry if these seem abstract - we’ll explain each one with concrete examples as we go.

Term
Scalar
Definition
A single number
Example
42, 3.14
Term
Vector
Definition
A 1-dimensional list of numbers
Example
[1, 2, 3, 4, 5]
Term
Matrix
Definition
A 2-dimensional grid of numbers
Example
[[1, 2], [3, 4]]
Term
Tensor
Definition
An n-dimensional array of numbers (generalizes all of the above)
Example
Any of the above, or higher dimensions
Term
Shape
Definition
The dimensions of a tensor as a tuple
Example
[2, 3] means 2 rows, 3 columns
Term
Rank
Definition
The number of dimensions a tensor has (also called order or degree)
Example
A matrix has rank 2
Term
Dimension
Definition
One axis of a tensor
Example
A [2, 3, 4] tensor has 3 dimensions
Term
Broadcasting
Definition
Automatically expanding smaller tensors to match larger ones
Example
Shapes [1, 3] and [2, 1] broadcast to [2, 3]

Further reading:

Part 1: What is a Tensor?

Before we talk about type safety, let’s make sure we understand what we’re making type-safe.

The Basics: Scalars, Vectors, and Matrices

A scalar is just a single number:

4242

It has no dimensions - you can think of it as a “point” in number-space. Its shape is [] (empty), and its rank is 0.

A vector is a list of numbers:

v⃗=[12345]\vec{v} = \begin{bmatrix} 1 & 2 & 3 & 4 & 5 \end{bmatrix}

This vector has 5 elements. Its shape is [5], and its rank is 1 (one dimension).

A matrix is a grid of numbers with rows and columns:

M=[123 456]M = \begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \end{bmatrix}

This matrix has 2 rows and 3 columns. Its shape is [2, 3], and its rank is 2 (two dimensions: rows and columns).

What is a tensor - visualization

Tensors: The General Case

A tensor is the generalization of all of these. It’s an n-dimensional array of numbers.

  • A scalar is a rank-0 tensor (shape: [])
  • A vector is a rank-1 tensor (shape: [5] for 5 elements)
  • A matrix is a rank-2 tensor (shape: [2, 3] for 2 rows, 3 columns)
  • A rank-3 tensor might have shape [2, 3, 4] - think of it as 2 matrices, each with 3 rows and 4 columns

New to tensors? Think of them like LEGO:

  • A scalar (42) is a single 1x1 brick
  • A vector ([1, 2, 3]) is a 1x3 row of bricks
  • A matrix ([[1,2], [3,4]]) is a 2x2 plate
  • A tensor is any LEGO build - no matter how big or layered!

The shape tells you the size of each layer. A [2, 3, 4] tensor is like 2 plates stacked, each plate being a 3x4 grid.

Rank = number of “layers of brackets”:

  • 42 -> [] (rank 0)
  • [1, 2] -> [2] (rank 1)
  • [[1, 2], [3, 4]] -> [2, 2] (rank 2)

In machine learning, we work with tensors constantly:

  • An image might be shape [3, 224, 224] - 3 color channels, 224x224 pixels
  • A batch of images might be [32, 3, 224, 224] - 32 images
  • A language model’s attention weights might be [batch, heads, seq_len, seq_len]

Why Shapes Matter

Here’s the thing about tensor operations: shapes must be compatible.

When you multiply two matrices:

AmimesnimesBnimesp=CmimespA_{m imes n} imes B_{n imes p} = C_{m imes p}
[2, 3] x [3, 4] -> [2, 4]  // Works!

The inner dimensions (nn and nn) must match. The result has the outer dimensions (mimespm imes p).

But this doesn’t work:

[2, 3] x [5, 4] -> ???  // Error!

The inner dimensions (3 and 5) don’t match. This is a shape error.

In Python’s PyTorch, you only find out about shape errors when you run the code. Our goal is to catch them at compile time.

Part 2: The Shape Problem

Let’s look at a real example of how shape errors happen.

A Simple Neural Network Layer

function linearLayer(input, weights, bias) {
  // input shape: [batch_size, in_features]
  // weights shape: [in_features, out_features]
  // bias shape: [out_features]

  const output = input.matmul(weights);  // [batch_size, out_features]
  return output.add(bias);
}

This looks fine. But what if someone calls it wrong?

const input = torch.randn(32, 128);    // 32 samples, 128 features
const weights = torch.randn(64, 256);  // Oops! Should be [128, 256]
const bias = torch.randn(256);

linearLayer(input, weights, bias);  // Runtime error!

The error is subtle. The weights should be [128, 256] to match the input’s 128 features, but someone wrote [64, 256].

What We Want

In torch.js, the function signature tells TypeScript about the shape requirements:

function linearLayer<B extends number, I extends number, O extends number>(
  input: Tensor<[B, I]>,
      // Shape is [batch, in_features]
  weights: Tensor<[I, O]>,
    // Shape is [in_features, out_features] - note the I!
  bias: Tensor<[O]>           // Shape is [out_features] - note the O!
): Tensor<[B, O]> {           // Result is [batch, out_features]
  // ...
}

Now TypeScript understands that the second dimension of input must equal the first dimension of weights. If they don’t match, you get a compile-time error.

const input = torch.randn(32, 128);    // Tensor<[32, 128]>
const weights = torch.randn(64, 256);  // Tensor<[64, 256]>

linearLayer(input, weights, bias);
//          ^^^^^^
// Error: Tensor<[64, 256]> is not assignable to Tensor<[128, O]>

The bug is caught before you run any code.

The shape problem in tensor operations

The Challenge

Making this work requires teaching TypeScript to:

  1. Track tensor shapes as types: Tensor<[2, 3]> not just Tensor
  2. Compute output shapes from input shapes
  3. Produce readable errors when shapes don’t match
  4. Parse string-based notations like 'ij,jk->ik'

Let’s learn how to do each of these.

Part 3: TypeScript Types 101

Before we dive into the advanced stuff, let’s make sure we have a solid foundation in TypeScript’s type system. If you already know TypeScript well, feel free to skim this section.

Types Describe Values

At its simplest, a type describes what kind of value something can be:

const name: string = "Alice";      // A string
const age: number = 30;            // A number
const active: boolean = true;      // A boolean

Literal Types

TypeScript can be more specific than just “string” or “number”. It can track the exact value:

const direction: "north" = "north";  // Only "north", not any string
const count: 42 = 42;                // Only 42, not any number

This is called a literal type. This is crucial for our shape tracking - we need Tensor<[2, 3]>, not Tensor<number[]>.

Tuple Types

An array type like number[] means “an array of numbers of any length.” But a tuple type specifies the exact length and type of each position:

const point: [number, number] = [10, 20];        // Exactly 2 numbers
const rgb: [number, number, number] = [255, 0, 0]; // Exactly 3 numbers

For tensor shapes, we use tuples of literal numbers:

type Shape1 = [2, 3];      // A 2x3 shape
type Shape2 = [32, 3, 224, 224];  // A batch of images

Generic Types

Generics let types be parameterized:

type Box<T> = { value: T };

type StringBox = Box<string>;  // { value: string }
type NumberBox = Box<number>;  // { value: number }

Our Tensor type is generic over its shape:

type Tensor<Shape extends readonly number[]> = {
  shape: Shape;
  // ... other properties
};

type Matrix = Tensor<[2, 3]>;  // A 2x3 tensor
🚀

Shape Inference Sandbox

Hover over variables in this live editor to see how torch.js tracks shapes through every operation.

TypeScript types 101

Conditional Types

Here’s where it gets interesting. TypeScript can make decisions at the type level:

type IsString<T> = T extends string ? "yes" : "no";

type A = IsString<"hello">;  // "yes"
type B = IsString<42>;       // "no"

The extends keyword checks if one type is assignable to another. If T can be assigned to string, the result is "yes", otherwise "no".

Inferring Types

We can extract parts of types using infer:

type FirstElement<T> = T extends [infer First, ...any[]] ? First : never;

type A = FirstElement<[1, 2, 3]>;  // 1
type B = FirstElement<["a", "b"]>; // "a"

This says: “If T is a tuple, extract the first element and call it First.”

Template Literal Types

TypeScript can manipulate strings at the type level:

type Greeting<Name extends string> = "Hello, ${string}!" extends `Hello, ${Name}!` ? `Hello, ${Name}!` : never;

type A = Greeting<"World">;  // "Hello, World!"
type B = Greeting<"Alice">;  // "Hello, Alice!"

We can also pattern match on strings:

type GetName<S extends string> = S extends `Hello, ${infer Name}!` ? Name : never;

type A = GetName<"Hello, World!">;  // "World"
type B = GetName<"Hello, Alice!">;  // "Alice"
type C = GetName<"Goodbye!">;       // never (doesn't match pattern)

This is the foundation for parsing einsum equations like 'ij,jk->ik'.

Beyond tensors: This same technique powers type-safe routing in web frameworks. You can parse URL parameters at compile time:

// Extract route parameters from a URL pattern
type ExtractParams<T extends string> =
  T extends `${string}:${infer Param}/${infer Rest}`
    ? Param | ExtractParams<Rest>
    : T extends `${string}:${infer Param}`
    ? Param
    : never;

type Params = ExtractParams<'/users/:id/posts/:postId'>;
//   ^? 'id' | 'postId'

// Now your route handlers are type-safe!
function handleRoute<T extends string>(
  pattern: T,
  handler: (params: Record<ExtractParams<T>, string>) => void
) { /* ... */ }

handleRoute('/users/:id', (params) => {
  console.log(params.id);      // OK
  console.log(params.postId);  // Error: 'postId' doesn't exist
});

Libraries like tRPC, Hono, and many others use exactly this pattern. You’re learning techniques used in production by millions of developers.

Recursive Types

Types can reference themselves, enabling iteration:

type Countdown<N extends number, Acc extends any[] = []> =
  Acc['length'] extends N
    ? Acc
    : Countdown<N, [...Acc, any]>;

type Three = Countdown<3>;  // [any, any, any]

This builds a tuple of length N by recursively adding elements until Acc['length'] equals N.

Putting It Together

With these tools, TypeScript’s type system is Turing complete - it can compute anything a regular program can compute (within recursion limits). We’ll use this power to:

  1. Parse strings (using template literal types and conditional types)
  2. Do arithmetic (using tuple lengths)
  3. Transform shapes (using recursive types)

Let’s start building!

Part 4: Building Blocks - Type-Level Arithmetic

TypeScript doesn’t have built-in type-level arithmetic. You can’t write type Sum = 2 + 3. But we can build it ourselves using a clever trick: tuple lengths.

The Key Insight

A tuple’s length property is a literal number type:

type T = [any, any, any];
type Len = T['length'];  // 3 (not just 'number', but literally '3')
🚀

Type-Level Math

Explore the magic of tuple length arithmetic. Change the numbers to see the type system recalculate the sum.

So if we want to represent the number 5 at the type level, we can use a tuple of length 5:

type Five = [any, any, any, any, any];
type N = Five['length'];  // 5

Building Tuples of Any Length

First, we need a way to create a tuple of length N:

type TupleOf<N extends number, Acc extends any[] = []> =
  Acc['length'] extends N    // Is our accumulator the right length?
    ? Acc                    // Yes! Return it
    : TupleOf<N, [...Acc, any]>;  // No, add one element and recurse

Let’s trace through TupleOf<3>:

TupleOf<3, []>
  -> Acc['length'] is 0, not 3
  -> TupleOf<3, [any]>
    -> Acc['length'] is 1, not 3
    -> TupleOf<3, [any, any]>
      -> Acc['length'] is 2, not 3
      -> TupleOf<3, [any, any, any]>
        -> Acc['length'] is 3
        -> Return [any, any, any]

Now TupleOf<3> gives us [any, any, any].

Addition: Concatenate Tuples

To add two numbers, we concatenate their tuple representations:

type Add<A extends number, B extends number> =
  [...TupleOf<A>, ...TupleOf<B>]['length'];

Let’s trace Add<2, 3>:

Add<2, 3>
  -> [...TupleOf<2>, ...TupleOf<3>]['length']
  -> [...[any, any], ...[any, any, any]]['length']
  -> [any, any, any, any, any]['length']
  -> 5

We just did 2 + 3 = 5 entirely at the type level!

Subtraction: Destructure Tuples

Subtraction is trickier. We use pattern matching:

type Subtract<A extends number, B extends number> =
  TupleOf<A> extends [...TupleOf<B>, ...infer Rest]
    ? Rest['length']
    : 0;  // Return 0 if B > A (no negative numbers)

This asks: “Can we split a tuple of length A into a tuple of length B plus some remainder?” If yes, the answer is the remainder’s length.

Let’s trace Subtract<5, 2>:

Subtract<5, 2>
  -> TupleOf<5> extends [...TupleOf<2>, ...infer Rest]
  -> [any, any, any, any, any] extends [...[any, any], ...infer Rest]
  -> Yes! Rest = [any, any, any]
  -> Rest['length'] = 3

Comparison: Is A Less Than B?

We often need to check bounds. Is index 5 valid for dimension size 4?

type LessThan<A extends number, B extends number> =
  A extends B
    ? false  // Equal, so not less than
    : TupleOf<B> extends [...TupleOf<A>, ...infer Rest]
      ? Rest extends [any, ...any[]]  // Is there at least one element left?
        ? true   // Yes! B > A, so A < B
        : false
      : false;

The logic: if we can split B into A plus a non-empty remainder, then A < B.

type T1 = LessThan<3, 5>;  // true (3 < 5)
type T2 = LessThan<5, 3>;  // false (5 is not < 3)
type T3 = LessThan<3, 3>;  // false (3 is not < 3)

Multiplication: Repeated Addition

Multiplication is addition in a loop:

type Multiply<A extends number, B extends number> =
  B extends 0
    ? 0
    : Add<A, Multiply<A, Subtract<B, 1>>>;

This computes A x B as A + A + A + ... (B times).

Multiply<3, 4>
  -> Add<3, Multiply<3, 3>>
  -> Add<3, Add<3, Multiply<3, 2>>>
  -> Add<3, Add<3, Add<3, Multiply<3, 1>>>>
  -> Add<3, Add<3, Add<3, Add<3, Multiply<3, 0>>>>>
  -> Add<3, Add<3, Add<3, Add<3, 0>>>>
  -> Add<3, Add<3, Add<3, 3>>>
  -> Add<3, Add<3, 6>>
  -> Add<3, 9>
  -> 12

A Complete Arithmetic Library

Here’s our toolkit so far:

// Create tuple of length N
type TupleOf<N extends number, T extends any[] = []> =
  T['length'] extends N ? T : TupleOf<N, [...T, any]>;

// Addition
type Add<A extends number, B extends number> =
  [...TupleOf<A>, ...TupleOf<B>]['length'] extends infer R extends number ? R : never;

// Subtraction (returns 0 if B > A)
type Subtract<A extends number, B extends number> =
  TupleOf<A> extends [...TupleOf<B>, ...infer Rest] ? Rest['length'] : 0;

// Comparison
type LessThan<A extends number, B extends number> =
  A extends B ? false :
  TupleOf<B> extends [...TupleOf<A>, infer _, ...any[]] ? true : false;

// Multiplication
type Multiply<A extends number, B extends number> =
  B extends 0 ? 0 : Add<A, Multiply<A, Subtract<B, 1>>>;

Practical Limits

TypeScript has recursion limits (around 500-1000 levels depending on complexity). This means our arithmetic works well for small numbers (shapes rarely exceed a few dimensions), but you can’t compute TupleOf<10000>.

For our tensor shape calculations, this is fine - shapes like [32, 3, 224, 224] have only 4 dimensions, even if the individual dimension sizes are large.

Why This Matters

With this arithmetic, we can now:

  • Add shapes: [2, 3] + [4] -> [2, 3, 4] (concatenation)
  • Compute slice sizes: end - start
  • Validate bounds: index < dimSize
  • Compute products: channel x height x width when flattening

Beyond tensors: Type-level arithmetic is useful anywhere you need to enforce numeric constraints. Here’s how you might limit GraphQL query depth to prevent DoS attacks:

// Limit nested query depth at compile time
type MaxDepth = 3;

type DeepQuery<T, Depth extends number = MaxDepth> =
  Depth extends 0
    ? never  // Too deep! Block this query shape
    : {
        [K in keyof T]?: T[K] extends object
          ? DeepQuery<T[K], Subtract<Depth, 1>>  // Recurse with depth - 1
          : T[K];
      };

// This compiles - depth 2
const valid: DeepQuery<{ user: { posts: { title: string } } }> = {
  user: { posts: { title: 'Hello' } }
};

// This would error - depth 4 exceeds limit of 3
// const invalid: DeepQuery<{ a: { b: { c: { d: string } } } }>;

The same Subtract type we built for tensor shapes enforces API security policies. Type-level arithmetic isn’t just academic - it solves real problems.

Let’s put it to use!

Part 5: Branded Error Types

When something goes wrong, we want clear error messages. But TypeScript’s default behavior isn’t always helpful.

Making Errors Helpful (Not Just never)

Consider this type that requires two numbers to be equal:

type RequireEqual<A extends number, B extends number> =
  A extends B ? A : never;

type Good = RequireEqual<3, 3>;  // 3
type Bad = RequireEqual<3, 5>;   // never

When you use Bad somewhere, TypeScript just says:

Type 'never' is not assignable to type 'number'

That’s useless! We want it to say:

matmul error: inner dimensions 3 and 5 don't match ([2,3] vs [5,4])

To do that, we use a trick called branding - a way to “tag” error types with descriptive messages.

How Branding Works

A branded type adds extra information to a type without changing its runtime behavior. Here’s the pattern:

// Create a unique symbol for branding
declare const ShapeError: unique symbol;

// Our error type extends the expected type (number[]) but has extra properties
type ErrorShape<Message extends string> = readonly number[] & {
  readonly [ShapeError]: Message;
  readonly __isShapeError: true;
};

Now we can create descriptive error types:

type matmul_error_inner_dimensions_do_not_match<
  K1 extends number,  // First matrix's inner dim
  K2 extends number,  // Second matrix's inner dim
  Shape1 extends readonly number[],
  Shape2 extends readonly number[]
> = ErrorShape<
  `inner dimensions ${K1} and ${K2} do not match`
> & {
  readonly _shape1: Shape1;
  readonly _shape2: Shape2;
};

How It Works

Let’s trace through what happens:

type MatmulShape<A extends readonly number[], B extends readonly number[]> =
  A extends readonly [infer M extends number, infer K1 extends number]
    ? B extends readonly [infer K2 extends number, infer N extends number]
      ? K1 extends K2
        ? readonly [M, N]  // Success! Return output shape
        : matmul_error_inner_dimensions_do_not_match<K1, K2, A, B>  // Error type
      : never
    : never;

// Using it:
type Good = MatmulShape<[2, 3], [3, 4]>;  // [2, 4]
type Bad = MatmulShape<[2, 3], [5, 4]>;   // matmul_error_inner_dimensions_do_not_match<3, 5, [2,3], [5,4]>

When you try to use Bad:

function useTensor(t: Tensor<readonly number[]>) { ... }

declare const result: Tensor<MatmulShape<[2, 3], [5, 4]>>;
useTensor(result);
//        ^^^^^^
// Error: Type 'matmul_error_inner_dimensions_do_not_match<3, 5, [2,3], [5,4]>'
// is not assignable to type 'readonly number[]'

The error message includes the full type name, which tells you exactly what went wrong!

Why We Extend readonly number[]

You might wonder: why does ErrorShape extend readonly number[]?

The reason is that our Tensor type looks like this:

interface Tensor<S extends readonly number[]> {
  shape: S;
  // ...
}

The shape type must extend readonly number[]. If our error type didn’t extend this, TypeScript would reject it immediately with a generic error, losing our nice message.

By extending readonly number[] but adding branded properties, the error type:

  1. Satisfies the S extends readonly number[] constraint
  2. Is incompatible with actual shape usage (due to branded properties)
  3. Shows our custom message when incompatibility is detected

A Library of Error Types

Here are some error types we use:

// Matrix multiplication dimension mismatch
export type matmul_error_inner_dimensions_do_not_match<
  K1 extends number,
  K2 extends number,
  Shape1 extends readonly number[],
  Shape2 extends readonly number[]
> = ErrorShape<
  `matmul_error_inner_dimensions_do_not_match<${K1}, ${K2}>`
> & {
  readonly _shape1: Shape1;
  readonly _shape2: Shape2;
};

// Dimension index out of range
export type dimension_error_out_of_range<
  Dim extends number,
  Rank extends number
> = ErrorShape<
  `dimension_error_out_of_range<dim=${Dim}, rank=${Rank}>`
>;

// Broadcast incompatibility
export type broadcast_error_incompatible_dimensions<
  D1 extends number,
  D2 extends number
> = ErrorShape<
  `broadcast_error_incompatible_dimensions<${D1}, ${D2}>`
>;

// Index out of bounds for .at()
export type at_error_index_out_of_bounds<
  Index extends number,
  DimSize extends number
> = ErrorShape<
  `at_error_index_out_of_bounds<index=${Index}, size=${DimSize}>`
>;

Detecting Errors

Sometimes we need to check if a type is an error:

type IsShapeError<T> = T extends { readonly __isShapeError: true } ? true : false;

type A = IsShapeError<[2, 3]>;  // false
type B = IsShapeError<matmul_error_inner_dimensions_do_not_match<3, 5, [2,3], [5,4]>>;  // true

This is useful for validation chains where we want to stop at the first error.

The User Experience

Here’s an important detail about how these errors work. When you write an invalid operation, TypeScript doesn’t error immediately:

const a = torch.zeros(2, 3);
const b = torch.zeros(5, 4);
const c = a.matmul(b);  // No error here! TypeScript is happy to assign this.
//    ^? Tensor<matmul_error_inner_dimensions_do_not_match<3, 5, [2,3], [5,4]>>

The variable c gets assigned the error type, but TypeScript doesn’t complain yet. Why? Because TypeScript only errors when there’s a type incompatibility - and assigning a value to a variable with an inferred type is always allowed.

The error surfaces when you try to use the tensor:

const c = a.matmul(b);  // c has the error type, but no error yet

// Error appears when you try to USE c:
c.mul(2);
// ^ Error: Property 'mul' does not exist on type
//   'Tensor<matmul_error_inner_dimensions_do_not_match<3, 5, [2,3], [5,4]>>'

// Or pass it to a function:
someFunction(c);
// ^ Error: Type 'matmul_error_inner_dimensions_do_not_match<...>'
//   is not assignable to type 'readonly number[]'

This is actually a good design. The error message appears at the point where you’re trying to do something with the bad value, which is often closer to where you need to fix the code. And the error type name tells the whole story:

  • matmul_error - it’s a matrix multiplication error
  • inner_dimensions_do_not_match - the inner dimensions don’t match
  • <3, 5, [2,3], [5,4]> - specifically, 3 != 5, and here are the full shapes

Much better than just “Type ’never’ is not assignable”!

Beyond tensors: Branded error types work for any domain. Imagine a type-safe SQL query builder:

// Define your schema
type UsersTable = { id: number; name: string; email: string };
type PostsTable = { id: number; userId: number; title: string };

type Schema = {
  users: UsersTable;
  posts: PostsTable;
};

// Error type for invalid columns
type sql_error_column_not_in_table<
  Col extends string,
  Table extends string
> = { readonly __brand: `Column '${Col}' does not exist in table '${Table}'` };

// Type-safe select
type ValidColumns<T extends keyof Schema> = keyof Schema[T];

function select<
  T extends keyof Schema,
  C extends ValidColumns<T>
>(table: T, columns: C[]): Pick<Schema[T], C>[] { /* ... */ }

// This works
select('users', ['id', 'name']);

// This errors with a clear message
select('users', ['id', 'namee']);
//                     ^^^^^^^ Argument of type '"namee"' is not
// assignable to parameter of type '"id" | "name" | "email"'

Libraries like Drizzle ORM and Kysely use similar patterns to catch SQL mistakes at compile time, not when your production database throws an error at 3am.

🚀

Break the Type System

Intentionally create a shape mismatch and see how the branded error type guides you to the solution.

Part 6: Einsum - Parsing Math Notation

Now for the fun part: parsing a domain-specific language at compile time!

What is Einsum?

Einstein summation notation (einsum) is a powerful way to express tensor operations. Instead of calling specific functions like matmul, transpose, or sum, you describe the operation using index labels.

Let’s see some examples, with the equivalent code without einsum to make it clear what’s happening:

// Matrix multiplication: C[i,k] = sum over j of A[i,j] * B[j,k]
torch.einsum('ij,jk->ik', A, B)
// Equivalent without einsum:
A.matmul(B)

// Batch matrix multiplication (multiply many matrices at once)
torch.einsum('bij,bjk->bik', A, B)
// Equivalent without einsum:
torch.bmm(A, B)

// Transpose (swap rows and columns)
torch.einsum('ij->ji', A)
// Equivalent without einsum:
A.t()       // or: A.transpose(0, 1)

// Sum all elements to a scalar
torch.einsum('ij->', A)
// Equivalent without einsum:
A.sum()

// Sum along one axis
torch.einsum('ij->i', A)
// Equivalent without einsum:
A.sum(1)    // sum along axis 1 (columns)

// Dot product (multiply element-wise, then sum)
torch.einsum('i,i->', a, b)
// Equivalent without einsum:
a.mul(b).sum()   // or: torch.dot(a, b)

// Outer product (every combination of elements)
torch.einsum('i,j->ij', a, b)
// Equivalent without einsum:
a.unsqueeze(1).mul(b.unsqueeze(0))   // or: torch.outer(a, b)

// More complex: matrix-vector multiplication
torch.einsum('ij,j->i', A, v)
// Equivalent without einsum:
A.matmul(v)   // or: torch.mv(A, v)

// Even more complex: batch outer product
torch.einsum('bi,bj->bij', a, b)
// Equivalent without einsum:
a.unsqueeze(2).mul(b.unsqueeze(1))

The notation works like this:

  • Each tensor gets a subscript (like ij or bjk)
  • Each letter represents a dimension (called an index)
  • The arrow -> separates inputs from outputs
  • Indices that appear in inputs but not outputs are summed over (this is the “summation” in Einstein summation)
  • Indices with the same letter must have the same size

Mathematical notation: Matrix multiplication ij,jk->ik means:

Cik=sumjAijcdotBjkC_{ik} = sum_j A_{ij} cdot B_{jk}

The index jj appears in both inputs but not the output, so we sum over it.

Why Use Einsum?

You might wonder: if there’s always an equivalent without einsum, why bother?

Einsum is more flexible and often clearer for complex operations:

// Contract two 4D tensors along specific dimensions
// Without einsum - hard to read!
torch.tensordot(A, B, [[1, 3], [0, 2]]).permute(0, 2, 1, 3)

// With einsum - the intention is clear
torch.einsum('aibj,ibjc->ac', A, B)

Our Goal

We want to parse any einsum equation at compile time and:

  1. Validate that the equation makes sense
  2. Check that tensor ranks match subscript lengths
  3. Compute the output shape
const a = torch.zeros(2, 3);  // Tensor<[2, 3]>
const b = torch.zeros(3, 4);  // Tensor<[3, 4]>

// TypeScript should know the result is Tensor<[2, 4]>
const c = torch.einsum('ij,jk->ik', a, b);

What Does “Parsing” Mean?

When you write a program, your code is just text - a string of characters. The computer needs to understand what that text means. This process of turning text into structured data is called parsing.

For example, when you write 2 + 3, the parser recognizes:

  • 2 is a number
  • + is an operator
  • 3 is another number

And it builds a structure like: { operator: '+', left: 2, right: 3 }.

We’re going to do this same thing, but entirely within TypeScript’s type system. Instead of parsing at runtime, we’ll parse at compile time. The “program” we’re parsing is the einsum equation string.

The Parsing Strategy

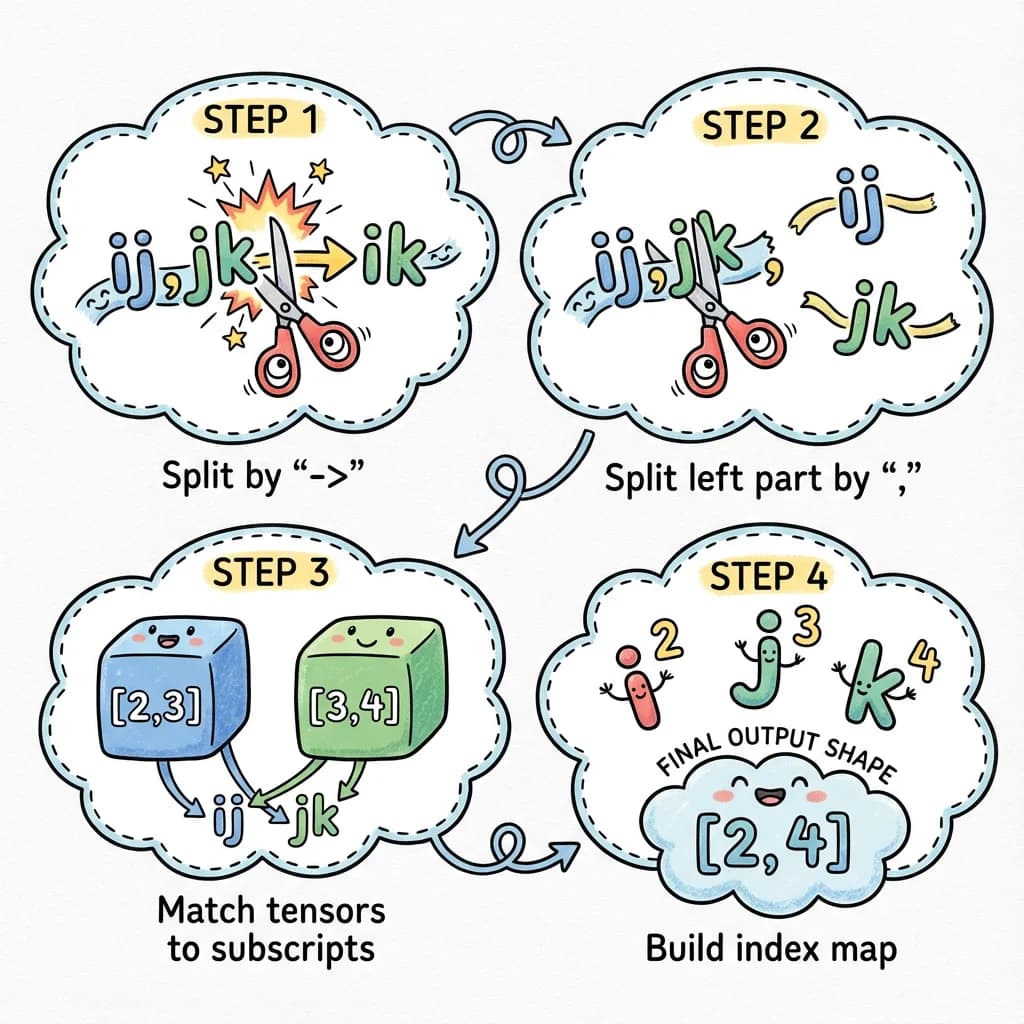
Let’s think about what we need to do with 'ij,jk->ik':

Input equation:     'ij,jk->ik'
Input shapes:       [2, 3] and [3, 4]

Step 1: Split on '->'
  -> inputs: 'ij,jk'
  -> output: 'ik'

Step 2: Split inputs on ','
  -> ['ij', 'jk']

Step 3: Pair subscripts with shapes
  -> 'ij' goes with [2, 3]
  -> 'jk' goes with [3, 4]

Step 4: Build an index->size map
  -> 'i' -> 2 (first dim of first tensor)
  -> 'j' -> 3 (second dim of first tensor)
  -> 'j' -> 3 (first dim of second tensor) - same!
  -> 'k' -> 4 (second dim of second tensor)

Step 5: Compute output by looking up each output index
  -> 'i' -> 2
  -> 'k' -> 4
  -> Output shape: [2, 4]

This is the key insight: we build a lookup table mapping index letters to their sizes, then use that table to compute the output shape.

Now let’s implement each step as a TypeScript type!

Step 1: Splitting on the Arrow

First, let’s split 'ij,jk->ik' into inputs ('ij,jk') and output ('ik'):

type SplitArrow<S extends string> =
  S extends `${infer Inputs}->${infer Output}`
    ? { inputs: Inputs; output: Output; explicit: true }
    : { inputs: S; output: never; explicit: false };

SplitArrow type matching visualization

Let’s trace through SplitArrow<'ij,jk->ik'>:

SplitArrow<'ij,jk->ik'>
  -> Does 'ij,jk->ik' match pattern `
      ${infer Inputs}->${infer Output}
    `?
  -> Yes! Inputs = 'ij,jk', Output = 'ik'
  -> Return { inputs: 'ij,jk'; output: 'ik'; explicit: true }

If there’s no arrow (implicit output), we handle that too:

SplitArrow<'ij,jk'>
  -> Does 'ij,jk' match pattern `
      ${infer Inputs}->${infer Output}
    `?
  -> No arrow found
  -> Return { inputs: 'ij,jk'; output: never; explicit: false }

Step 2: Splitting on Commas

Now we split 'ij,jk' into ['ij', 'jk']:

type SplitComma<S extends string> =
  S extends `${infer First},${infer Rest}`
    ? [First, ...SplitComma<Rest>]  // Found comma, recurse on rest
    : S extends ''
      ? []           // Empty string
      : [S];         // No comma, single element

SplitComma type parsing visualization

Tracing SplitComma<'ij,jk,kl'>:

SplitComma<'ij,jk,kl'>
  -> 'ij,jk,kl' matches `
      ${infer First},${infer Rest}
    `
  -> First = 'ij', Rest = 'jk,kl'
  -> Return ['ij', ...SplitComma<'jk,kl'>]
    -> SplitComma<'jk,kl'>
      -> First = 'jk', Rest = 'kl'
      -> Return ['jk', ...SplitComma<'kl'>]
        -> SplitComma<'kl'>
          -> No comma in 'kl'
          -> Return ['kl']
      -> Return ['jk', 'kl']
    -> Return ['ij', 'jk', 'kl']

Result: ['ij', 'jk', 'kl']

Step 3: Converting Strings to Character Arrays

To work with individual indices, we need to split a subscript like 'ijk' into ['i', 'j', 'k']:

type StringToChars<S extends string> =
  S extends 
    `
      ${infer C}${infer Rest}
    `
    ? [C, ...StringToChars<Rest>]
    : [];

StringToChars type parsing visualization

Tracing StringToChars<'ijk'>:

StringToChars<"ijk">
  -> "ijk" matches `${infer C}${infer Rest}`
  -> C = "i", Rest = "jk"
  -> ["i", ...StringToChars<"jk">]
    -> ["i", "j", ...StringToChars<"k">]
      -> ["i", "j", "k", ...StringToChars<"">]
        -> ["i", "j", "k"]

Result: ['i', 'j', 'k']

Beyond tensors: This string parsing pattern works for any DSL. Here’s how you might parse CSS values with units:

// Parse CSS values like '16px', '2rem', '100%'
type ParseCSSValue<S extends string> =
  S extends `${infer N}px`
    ? { value: N; unit: 'px' }
  : S extends `${infer N}rem`
    ? { value: N; unit: 'rem' }
  : S extends `${infer N}em`
    ? { value: N; unit: 'em' }
  : S extends `${infer N}%`
    ? { value: N; unit: '%' }
  : never;

type A = ParseCSSValue<'16px'>;   // { value: '16', unit: 'px' }
type B = ParseCSSValue<'2rem'>;   // { value: '2', unit: 'rem' }
type C = ParseCSSValue<'100%'>;   // { value: '100', unit: '%' }

// Use it for type-safe styling
function spacing<T extends string>(value: T): ParseCSSValue<T> {
  // ...
}

const padding = spacing('16px');
//    ^? { value: '16', unit: 'px' }

CSS-in-JS libraries like vanilla-extract and Panda CSS use similar techniques to provide autocomplete and catch invalid style values at compile time.

Step 4: Building an Index-to-Size Map

Here’s the key insight: we need to know what size each index represents. For equation 'ij,jk->ik' with shapes [2, 3] and [3, 4]:

  • Index i has size 2 (first dimension of first tensor)
  • Index j has size 3 (second dimension of first tensor, or first dimension of second tensor)
  • Index k has size 4 (second dimension of second tensor)

We build this map by pairing each character in a subscript with its corresponding dimension size:

type BuildIndexMap<
  Subscript extends string,
  Shape extends readonly number[]
> = BuildIndexMapHelper<StringToChars<Subscript>, Shape, 0>;

type BuildIndexMapHelper<
  Chars extends string[],
  Shape extends readonly number[],
  Idx extends number
> = Chars extends [infer C extends string, ...infer Rest extends string[]]
  ? [[C, Shape[Idx]], ...BuildIndexMapHelper<Rest, Shape, Add<Idx, 1>>]
  : [];

Let’s trace this for subscript 'ij' with shape [2, 3]:

BuildIndexMap<'ij', [2, 3]>
  -> BuildIndexMapHelper<['i', 'j'], [2, 3], 0>
    -> Chars = ['i', 'j'], first char is 'i'
    -> Shape[0] = 2
    -> [['i', 2], ...BuildIndexMapHelper<['j'], [2, 3], 1>]
      -> Chars = ['j'], first char is 'j'
      -> Shape[1] = 3
      -> [['j', 3], ...BuildIndexMapHelper<[], [2, 3], 2>]
        -> Chars is empty
        -> Return []
      -> Return [['j', 3]]
    -> Return [['i', 2], ['j', 3]]

Result: [['i', 2], ['j', 3]] - our index map!

Step 5: Merging Multiple Index Maps

For multiple input tensors, we build a map for each and merge them:

type MergeIndexMaps<
  Subscripts extends string[],
  Shapes extends readonly (readonly number[])[],
  Acc extends [string, number][] = []
> = Subscripts extends [infer Sub extends string, ...infer RestSubs extends string[]]
  ? Shapes extends [infer S extends readonly number[], ...infer RestShapes extends readonly (readonly number[])[]]
    ? MergeIndexMaps<RestSubs, RestShapes, [...Acc, ...BuildIndexMap<Sub, S>]>
    : Acc
  : Acc;

For ['ij', 'jk'] with shapes [[2, 3], [3, 4]]:

MergeIndexMaps<['ij', 'jk'], [[2, 3], [3, 4]], []>
  -> First subscript: 'ij', first shape: [2, 3]
  -> BuildIndexMap<'ij', [2, 3]> = [['i', 2], ['j', 3]]
  -> MergeIndexMaps<['jk'], [[3, 4]], [['i', 2], ['j', 3]]>
    -> First subscript: 'jk', first shape: [3, 4]
    -> BuildIndexMap<'jk', [3, 4]> = [['j', 3], ['k', 4]]
    -> MergeIndexMaps<[], [], [['i', 2], ['j', 3], ['j', 3], ['k', 4]]>
      -> No more subscripts
      -> Return [['i', 2], ['j', 3], ['j', 3], ['k', 4]]

Note: 'j' appears twice with the same size - that’s expected and correct!

Step 6: Looking Up Index Sizes

Now we need a function to look up an index’s size from the map:

type LookupIndex<Map extends [string, number][], Index extends string> =
  Map extends [[infer K, infer V extends number], ...infer Rest extends [string, number][]]
    ? K extends Index
      ? V  // Found it!
      : LookupIndex<Rest, Index>
    : number;  // Not found - return dynamic

Step 7: Computing Output Shape

Finally, we compute the output shape by looking up each output index:

type ComputeEinsumOutput<
  OutputSubscript extends string,
  IndexMap extends [string, number][]
> = ComputeOutputHelper<StringToChars<OutputSubscript>, IndexMap>;

type ComputeOutputHelper<
  Chars extends string[],
  IndexMap extends [string, number][]
> = Chars extends [infer C extends string, ...infer Rest extends string[]]
  ? [LookupIndex<IndexMap, C>, ...ComputeOutputHelper<Rest, IndexMap>]
  : [];

For output 'ik' with map [['i', 2], ['j', 3], ['j', 3], ['k', 4]]:

ComputeEinsumOutput<'ik', [['i', 2], ['j', 3], ['j', 3], ['k', 4]]>
  -> ComputeOutputHelper<['i', 'k'], map>
    -> First char: 'i'
    -> LookupIndex<map, 'i'> = 2
    -> [2, ...ComputeOutputHelper<['k'], map>]
      -> First char: 'k'
      -> LookupIndex<map, 'k'> = 4
      -> [4, ...ComputeOutputHelper<[], map>]
        -> Return []
      -> Return [4]
    -> Return [2, 4]

Result: [2, 4]

The Complete Einsum Parser

Now we can put all the pieces together into a single type that parses any einsum equation:

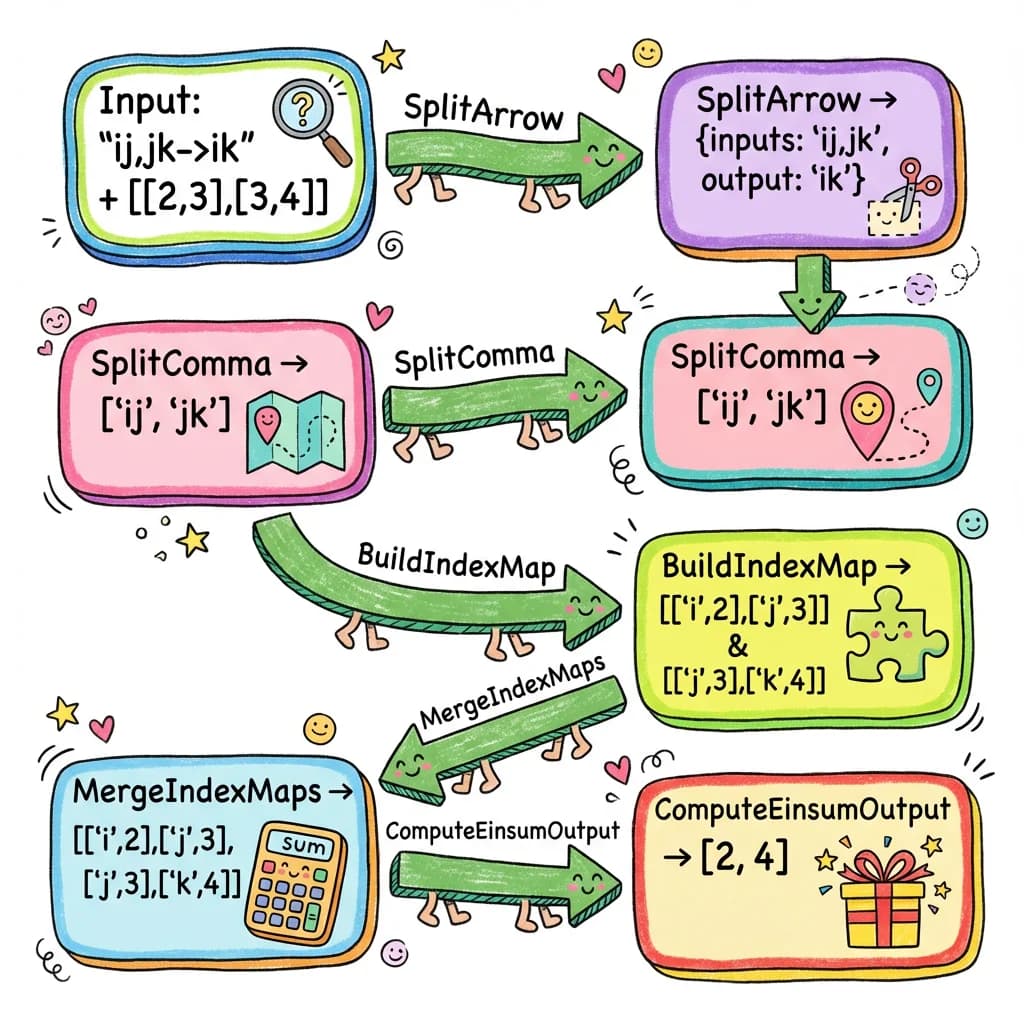
Complete einsum parser architecture

Here’s the type that orchestrates this entire flow:

export type ParsedEinsumShape<
  E extends string,
  Shapes extends readonly (readonly number[])[]
> =
  // Parse equation into inputs and output
  SplitArrow<E> extends { inputs: infer Inputs extends string; output: infer Output extends string }
    // Split inputs into subscripts
    ? SplitComma<Inputs> extends infer Subscripts extends string[]
      // Build merged index map from all inputs
      ? MergeIndexMaps<Subscripts, Shapes> extends infer IndexMap extends [string, number][]
        // Compute output shape from output subscript
        ? ComputeEinsumOutput<Output, IndexMap>
        : readonly number[]
      : readonly number[]
    : readonly number[];

Testing It

// Matrix multiplication: 'ij,jk->ik'
type T1 = ParsedEinsumShape<'ij,jk->ik', [[2, 3], [3, 4]]>;  // [2, 4]

// Batch matmul: 'bij,bjk->bik'
type T2 = ParsedEinsumShape<'bij,bjk->bik', [[5, 2, 3], [5, 3, 4]]>;  // [5, 2, 4]

// Dot product: 'i,i->'
type T3 = ParsedEinsumShape<'i,i->', [[3], [3]]>;  // [] (scalar)

// Outer product: 'i,j->ij'
type T4 = ParsedEinsumShape<'i,j->ij', [[2], [3]]>;  // [2, 3]

// Complex contraction: 'abc,bcd->ad'
type T5 = ParsedEinsumShape<'abc,bcd->ad', [[2, 3, 4], [3, 4, 5]]>;  // [2, 5]

// Trace (sum diagonal): 'ii->'
type T6 = ParsedEinsumShape<'ii->', [[3, 3]]>;  // [] (scalar)

// Sum over one axis: 'ij->i'
type T7 = ParsedEinsumShape<'ij->i', [[2, 3]]>;  // [2]

This handles arbitrary einsum patterns, not just common ones like matmul! Any valid einsum equation will get the correct output shape inferred at compile time.

🚀

Einsum Sandbox

Experiment with arbitrary Einstein notation patterns and watch the output shapes update instantly.

Parsing mathematical notation at compile time

Adding Validation

We should also validate:

  1. Subscript lengths match tensor ranks
  2. Repeated indices have consistent sizes
  3. Output indices exist in inputs
type ValidateEinsumRanks<
  Subscripts extends string[],
  Shapes extends readonly (readonly number[])[]
> = Subscripts extends [infer Sub extends string, ...infer RestSubs extends string[]]
  ? Shapes extends [infer S extends readonly number[], ...infer RestShapes extends readonly (readonly number[])[]]
    ? StringToChars<Sub>['length'] extends S['length']
      ? ValidateEinsumRanks<RestSubs, RestShapes>
      : einsum_error_subscript_rank_mismatch<Sub & string, S['length'], StringToChars<Sub>['length']>
    : true
  : true;

Using It

const a = torch.zeros(2, 3);    // Tensor<[2, 3]>
const b = torch.zeros(3, 4);    // Tensor<[3, 4]>
const c = torch.zeros(4, 5, 6); // Tensor<[4, 5, 6]>

// Standard matmul
const r1 = torch.einsum('ij,jk->ik', a, b);
//    ^? Tensor<[2, 4]>

// Three-way contraction
const r2 = torch.einsum('ij,jk,kl->il', a, b, torch.zeros(4, 7));
//    ^? Tensor<[2, 7]>

// Complex pattern
const r3 = torch.einsum('abc,bcd->ad', torch.zeros(2, 3, 4), torch.zeros(3, 4, 5));
//    ^? Tensor<[2, 5]>

// Rank mismatch
const r4 = torch.einsum('ijk,jk->ik', a, b);  // 'a' has rank 2, not 3
//    ^? einsum_error_subscript_rank_mismatch<'ijk', 2, 3>

We’ve built a complete compile-time parser for Einstein notation!

This exact approach is implemented in torch.js’s einsum-types.ts. You can see it in action with 24 test cases in einsum-types.test.ts - covering everything from simple matrix multiplication to complex multi-tensor contractions.

The key takeaway: parsing at the type level follows the same principles as runtime parsing. You break the input into tokens, build intermediate data structures (like our index map), and compute the result step by step. The difference is that we’re manipulating types instead of values.

Part 7: Einops - A Better Pattern Language

Now that we’ve mastered einsum, let’s look at einops - a library that takes tensor reshaping to the next level with a more readable, flexible syntax.

From Einsum to Einops

Einsum is great for describing computations (multiplications, sums, contractions). But what about reshaping operations that don’t involve computation, just rearranging data?

Consider flattening an image batch from [32, 3, 224, 224] to [32, 150528]:

// With regular PyTorch/torch.js - works but cryptic
images.reshape(32, -1)
images.view(images.shape[0], -1)
images.flatten(1)

// With einsum - doesn't work! Einsum is for computation, not reshaping.

// With einops - clear and self-documenting!
rearrange(images, 'b c h w -> b (c h w)')

The einops pattern 'b c h w -> b (c h w)' says exactly what’s happening:

  • Input has 4 named dimensions: batch, channels, height, width
  • Output has 2 dimensions: batch, and a composite of (channels x height x width)

What Einops Can Do

// Flatten spatial dimensions (our example above)
rearrange(images, 'b c h w -> b (c h w)')
// [32, 3, 224, 224] -> [32, 150528]
// Equivalent without einops:
images.reshape(32, 3 * 224 * 224)

// Transpose (reorder dimensions)
rearrange(images, 'b c h w -> b h w c')
// [32, 3, 224, 224] -> [32, 224, 224, 3]
// Equivalent without einops:
images.permute(0, 2, 3, 1)

// Split a dimension
rearrange(images, 'b (g c) h w -> b g c h w', { g: 3 })
// [32, 12, 224, 224] -> [32, 3, 4, 224, 224]
// Equivalent without einops:
images.reshape(32, 3, 4, 224, 224)

// Merge dimensions
rearrange(tensor, 'b g c h w -> b (g c) h w')
// [32, 3, 4, 224, 224] -> [32, 12, 224, 224]
// Equivalent without einops:
tensor.reshape(32, 12, 224, 224)

// Add a new dimension with repeat
repeat(images, 'b c h w -> b c h w n', { n: 5 })
// [32, 3, 224, 224] -> [32, 3, 224, 224, 5]
// Equivalent without einops:
images.unsqueeze(-1).expand(-1, -1, -1, -1, 5)

// Reduce (with operation like mean, sum, max)
reduce(images, 'b c h w -> b c', 'mean')
// [32, 3, 224, 224] -> [32, 3]
// Equivalent without einops:
images.mean([2, 3])

Why Einops is Better Than Manual Reshaping

The non-einops equivalents work, but:

  1. They’re not self-documenting: What does permute(0, 2, 3, 1) mean? You have to count dimensions.
  2. They’re error-prone: What if you mix up 2 and 3?
  3. They don’t work for unknown shapes: reshape(32, 3 * 224 * 224) hardcodes dimensions. Einops works with variables.
  4. They’re hard to verify: Is reshape(32, 12, 224, 224) correct? With einops, the pattern tells you.

Parsing Einops Patterns

The einops parser is similar to einsum, but more sophisticated:

  1. Tokens are space-separated (not single characters)
  2. Parentheses group dimensions for merging/splitting
  3. Axis names can be multi-character (batch not just b)
  4. Special tokens: ... (ellipsis), _ (anonymous), 1 (singleton)

We already built this in Part 6 with einsum! The same techniques apply:

// Tokenize: 'b (c h w) -> b flat'
// becomes: ['b', '(c h w)', '->', 'b', 'flat']

// Parse parentheses: '(c h w)' becomes composite type
// { type: 'composite', parts: ['c', 'h', 'w'] }

// Build axis map from input pattern and shape
// 'b c h w' with [32, 3, 224, 224]
// -> [['b', 32], ['c', 3], ['h', 224], ['w', 224]]

// Compute output shape from output pattern
// 'b (c h w)' -> [32, 3 * 224 * 224] -> [32, 150528]

Einops Implementation (Simplified)

The full implementation is in packages/torch.js/src/ops/einops-types.ts, but here’s the essence:

// Parse pattern into tokens
type ParsePattern<P extends string> = ParseTokens<SplitSpace<P>>;

// Build axis-to-size map
type BuildAxisSizeMap<
  Dims extends ParsedDim[],
  InputShape extends readonly number[]
> = /* map each axis name to its dimension size */;

// Compute composite size (multiply parts)
type ComputeCompositeSize<Parts extends string[], AxisMap> =
  /* e.g., (c h w) with c=3, h=224, w=224 -> 3 x 224 x 224 = 150528 */;

// Main entry point
export type RearrangeShape<
  Pattern extends string,
  InputShape extends Shape
> = /* parse -> validate -> compute output */;

Using Type-Safe Einops

const images = torch.zeros(32, 3, 224, 224);  // Tensor<[32, 3, 224, 224]>

// Flatten spatial dimensions
const flat = rearrange(images, 'b c h w -> b (c h w)');
//    ^? Tensor<[32, 150528]>

// Transpose to channels-last
const channelsLast = rearrange(images, 'b c h w -> b h w c');
//    ^? Tensor<[32, 224, 224, 3]>

// Patch-based splitting (for Vision Transformers)
const patches = rearrange(images, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', { p1: 16, p2: 16 });
//    ^? Tensor<[32, 196, 768]>

// Unknown axis
const bad = rearrange(images, 'b c h w -> b x');
//    ^? einops_error_undefined_axis<'x'>

// Dimension mismatch
const bad2 = rearrange(images, 'b c h -> b c');
//    ^? einops_error_dimension_mismatch<3, 4>
🚀

Einops Reshape Lab

Master the pattern language of Einops. Rearrange, split, and merge dimensions with live feedback.

The Power of Named Dimensions

Both einsum and einops share a key insight: naming dimensions makes code clearer and safer.

Approach
Indices
Code
x.permute(0, 2, 3, 1)
Self-documenting?
No
Approach
Named
Code
rearrange(x, 'b c h w -> b h w c')
Self-documenting?
Yes

When you read b c h w -> b h w c, you instantly know:

  • Input is batch x channels x height x width
  • Output moves channels to the end

When you read permute(0, 2, 3, 1), you have to mentally map numbers to dimensions.

Part 8: Practical Slicing with .at()

We’ve built type-safe einsum and einops. Now let’s connect them to everyday tensor operations with type-safe slicing.

Motivating Example: Working with Einops Results

Imagine you’ve used einops to process some images:

const images = torch.randn(32, 3, 224, 224);  // Batch of 32 RGB images

// Extract patches for a Vision Transformer
const patches = rearrange(images, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', { p1: 16, p2: 16 });
// patches shape: [32, 196, 768]
// - 32 images
// - 196 patches per image (14x14 grid)
// - 768 values per patch (16x16x3)

Now you want to:

  1. Get the first image’s patches: patches.at(0) -> [196, 768]
  2. Get the first patch of each image: patches.at(null, 0) -> [32, 768]
  3. Get patches 10-20 from the first 5 images: patches.at([0, 5], [10, 20]) -> [5, 10, 768]

Each of these should have a precisely known output shape.

Python’s Flexible Indexing

Python’s NumPy and PyTorch support powerful indexing syntax:

x[0]           # First element of first dimension
x[:, 0]        # First element of second dimension
x[1:5]         # Slice from index 1 to 5
x[..., 0]      # Last dimension, first element (ellipsis fills middle)
x[mask]        # Boolean masking

The .at() Method

In torch.js, we use .at() for advanced indexing with compile-time type checking:

const a = torch.zeros(4, 5, 6);  // Tensor<[4, 5, 6]>

// Integer indexing - REMOVES the dimension
a.at(0)            // -> Tensor<[5, 6]>       (first along dim 0)
a.at(0, 0)         // -> Tensor<[6]>          (first along dims 0 and 1)
a.at(0, 0, 0)      // -> Tensor<[]>           (scalar - all dimensions removed)

// null - KEEPS the dimension unchanged
a.at(null)         // -> Tensor<[4, 5, 6]>    (no change)
a.at(null, 0)      // -> Tensor<[4, 6]>       (keep dim 0, select from dim 1)
a.at(0, null, 0)   // -> Tensor<[5]>          (select dim 0 and 2, keep dim 1)

// Range [start, end] - keeps dimension but changes size
a.at([1, 3])       // -> Tensor<[2, 5, 6]>    (indices 1 and 2 from dim 0)
a.at(null, [0, 3]) // -> Tensor<[4, 3, 6]>    (indices 0, 1, 2 from dim 1)

// Ellipsis '...' - fills in remaining dimensions
a.at('...')        // -> Tensor<[4, 5, 6]>    (same as a)
a.at('...', 0)     // -> Tensor<[4, 5]>       (first from LAST dim)
a.at(0, '...')     // -> Tensor<[5, 6]>       (same as a.at(0))
a.at(0, '...', 0)  // -> Tensor<[5]>          (first from first AND last)
🚀

Indexing Playground

Explore the power of the .at() method. Try integer indexing, null for full slices, and the '...' ellipsis.

Index Specification Types

We model each kind of index:

type IndexSpec =
  | number                           // Select index (removes dimension)
  | readonly [number, number]        // Slice [start, end] (keeps dimension)
  | null                             // Keep entire dimension
  | '...'                            // Ellipsis (expand to fill remaining)

What Each Spec Does to a Dimension

Spec
number
Example
a.at(2)
Action
Select index 2
Result
Remove dimension
Spec
[start, end]
Example
a.at([1, 4])
Action
Slice indices 1,2,3
Result
Change size to end - start
Spec
null
Example
a.at(null)
Action
Keep as-is
Result
No change
Spec
'...'
Example
a.at('...', 0)
Action
Expand
Result
Special handling

Type-safe .at() indexing operations

Type-Level Implementation

The implementation mirrors what we built for einsum and einops:

// Apply a single spec to one dimension
type ApplyIndexSpec<DimSize extends number, Spec extends IndexSpec> =
  // Integer: check bounds, mark for removal
  Spec extends number
    ? LessThan<Spec, DimSize> extends true
      ? 'remove'
      : at_error_index_out_of_bounds<Spec, DimSize>
  // Range: compute new size
  : Spec extends readonly [infer Start extends number, infer End extends number]
    ? Subtract<End, Start>
  // Null: keep original
  : Spec extends null
    ? DimSize
  // Ellipsis: special marker
  : 'ellipsis';

Handling Ellipsis

Ellipsis (...) is the trickiest part. In a.at('...', 0), the ellipsis should expand to cover all dimensions except the last.

The algorithm:

  1. Count non-ellipsis specs after the ...
  2. Keep dimensions until we have exactly that many left
  3. Apply the remaining specs
type ApplyIndexSpecsWithEllipsis<
  S extends readonly number[],      // Remaining shape
  Specs extends readonly IndexSpec[] // Specs after ellipsis
> =
  // Have we used up enough dimensions?
  CountNonEllipsis<Specs>['length'] extends S['length']
    ? ApplyIndexSpecs<S, Specs>  // Yes, apply remaining specs
    : S extends readonly [infer First extends number, ...infer Rest extends number[]]
      ? [First, ...ApplyIndexSpecsWithEllipsis<Rest, Specs>]  // Keep this dim
      : [];

Tracing a.at('...', 0) on [4, 5, 6]:

Shape: [4, 5, 6], Specs after '...': [0]
  -> Non-ellipsis count: 1
  -> Shape length: 3, not equal to 1
  -> Keep 4, recurse with [5, 6]
    -> Shape length: 2, not equal to 1
    -> Keep 5, recurse with [6]
      -> Shape length: 1, equals 1!
      -> Apply spec 0 to dimension 6
      -> 0 < 6, so remove dimension
      -> Result: []
    -> Result: [5]
  -> Result: [4, 5]

Bounds Checking

When an index is out of bounds, we return a descriptive error:

const a = torch.zeros(4, 5, 6);

const b = a.at(10);  // Error!
//    ^? at_error_index_out_of_bounds<10, 4>
// "You tried to access index 10, but dimension has size 4"

const c = a.at(0, 100);  // Error!
//    ^? at_error_index_out_of_bounds<100, 5>

Real-World Example: Processing Transformer Output

Let’s tie it all together with a realistic example:

// Transformer output: [batch, sequence, hidden]
const output = torch.randn(8, 512, 768);

// Get the [CLS] token embedding (first token of each sequence)
const cls = output.at(null, 0);
// ^? Tensor<[8, 768]>

// Get first 10 tokens from all batches
const firstTokens = output.at(null, [0, 10]);
// ^? Tensor<[8, 10, 768]>

// Get the last token (using ellipsis)
const last = output.at('...', -1, null);  // Negative indexing works too!
// ^? Tensor<[8, 768]> 

// Process with einops, then slice
const reshaped = rearrange(output, 'b s (h d) -> b h s d', { h: 12 });
// ^? Tensor<[8, 12, 512, 64]>

const head0 = reshaped.at(null, 0);  // First attention head
// ^? Tensor<[8, 512, 64]>

High-Dimensional Support

The types work for tensors up to 8 dimensions:

const big = torch.zeros(2, 3, 4, 5, 6, 7, 8, 9);  // 8D tensor

big.at(0)                    // Tensor<[3, 4, 5, 6, 7, 8, 9]>
big.at(0, 0, 0, 0)           // Tensor<[6, 7, 8, 9]>
big.at('...', 0)             // Tensor<[2, 3, 4, 5, 6, 7, 8]>
big.at(0, '...', 0)          // Tensor<[3, 4, 5, 6, 7, 8]>

// Complex mixed indexing
big.at(0, [1, 2], null, 0, null, [0, 3], null, 0)
// ^? Tensor<[1, 4, 6, 3, 8]>

Part 9: Testing Type-Level Code

We’ve built complex types, but how do we test them? We can’t use console.log!

The Challenge

Type-level code has no runtime. We can’t write:

// This doesn't work!
test('Add<2, 3> equals 5', () => {
  expect(Add<2, 3>).toBe(5);  // Types aren't values! 
});

Strategy 1: Type Assertions with Assignability

We can test that types are correct by checking assignability:

function assertType<Expected>(): <Actual extends Expected>(actual: Actual) => void {
  return () => {};
}

// Usage
const a = torch.zeros(4, 5, 6);
const b = a.at(0);

// If b.shape is [5, 6], this compiles. If not, TypeScript errors.
assertType<readonly [5, 6]>()(b.shape);

The trick: assertType<Expected>() returns a function that accepts only types extending Expected. If the actual type doesn’t match, you get a compile error at the call site.

Strategy 2: Test Files That Should Compile

Create test files that exercise your types:

// tests/at-types.test.ts
import { describe, it, expect } from 'vitest';
import { zeros } from '../src/ops/creation';

describe('AtShape type inference', () => {
  it('at(0) on [4,5,6] -> [5,6]', () => {
    const a = zeros(4, 5, 6);
    const b = a.at(0);

    // Runtime check
    expect(b.shape).toEqual([5, 6]);

    // Type check - if wrong, this line won't compile
    assertType<readonly [5, 6]>()(b.shape);
  });

  it('at(0, 0, 0) on [4,5,6] -> [] (scalar)', () => {
    const a = zeros(4, 5, 6);
    const b = a.at(0, 0, 0);

    expect(b.shape).toEqual([]);
    assertType<readonly []>()(b.shape);
  });

  it("at('...', 0) on [4,5,6] -> [4,5]", () => {
    const a = zeros(4, 5, 6);
    const b = a.at('...', 0);

    expect(b.shape).toEqual([4, 5]);
    assertType<readonly [4, 5]>()(b.shape);
  });
});

These tests verify both runtime behavior AND compile-time types.

Strategy 3: Files That Should NOT Compile

For error types, we want to verify that bad code produces type errors. Create files in a type-errors/ directory:

// type-errors/at-index-out-of-bounds.ts
import { zeros } from '../src/ops/creation';

const a = zeros(4, 5, 6);

// @ts-expect-error - index 10 is out of bounds for dimension of size 4
const b = a.at(10);

// @ts-expect-error - index 20 is out of bounds for dimension of size 5
const c = a.at(0, 20);

The @ts-expect-error directive tells TypeScript: “The next line should have an error.” If there’s no error, TypeScript reports that as a problem!

Strategy 4: Running Type Error Tests

We use a test script that runs tsc on the error files:

// scripts/test-type-errors.ts
import { execSync } from 'child_process';
import { glob } from 'glob';

const errorFiles = glob.sync('type-errors/*.ts');

for (const file of errorFiles) {
  try {
    execSync(`npx tsc --noEmit ${file}`, { stdio: 'pipe' });
    console.log(`[PASS] ${file}`);
  } catch (error) {
    const output = error.stderr.toString();
    if (output.includes('error TS2578')) {
      // TS2578: Unused '@ts-expect-error' directive
      console.error(`[FAIL] ${file}: Expected error but none found`);
      process.exit(1);
    }
    console.log(`[PASS] ${file}`);
  }
}

Example Error Test Files

// type-errors/matmul-dimension-mismatch.ts
import { zeros } from '../src/ops/creation';

const a = zeros(2, 3);
const b = zeros(5, 4);

// @ts-expect-error - inner dimensions 3 and 5 don't match
const c = a.matmul(b);
// type-errors/einops-undefined-axis.ts
import { rearrange } from '../src/ops/einops';
import { zeros } from '../src/ops/creation';

const images = zeros(32, 3, 224, 224);

// @ts-expect-error - 'x' is not defined in input pattern
const bad = rearrange(images, 'b c h w -> b x');
// type-errors/einsum-operand-count.ts
import { einsum, zeros } from '../src';

const a = zeros(2, 3);

// @ts-expect-error - equation expects 2 operands but got 1
const result = einsum('ij,jk->ik', a);

Strategy 5: Vitest Type Testing

Vitest has built-in support for type testing:

// tests/shapes.test-d.ts
import { expectTypeOf, test } from 'vitest';
import { zeros } from '../src';

test('zeros shape inference', () => {
  const a = zeros(2, 3);
  expectTypeOf(a.shape).toEqualTypeOf<readonly [2, 3]>();
});

test('matmul shape', () => {
  const a = zeros(2, 3);
  const b = zeros(3, 4);
  const c = a.matmul(b);
  expectTypeOf(c.shape).toEqualTypeOf<readonly [2, 4]>();
});

Our Testing Strategy

In torch.js, we use a combination:

  1. Regular tests with assertType: Verify shapes at runtime AND compile time
  2. type-errors/ directory: Verify that bad code produces errors
  3. CI integration: Run tsc --noEmit on all test files to catch regressions

This gives us confidence that our type-level code works correctly.

Beyond tensors: These testing techniques work for any custom types. Building a type-safe form library? Test it the same way:

// Test your type-safe form builder
import { expectTypeOf, test } from 'vitest';
import { createForm } from './form-builder';

test('form field types are inferred', () => {
  const form = createForm({
    name: { type: 'text', required: true },
    age: { type: 'number' },
    email: { type: 'email', required: true },
  });

  // Values should have correct types
  expectTypeOf(form.values).toEqualTypeOf<{
    name: string;
    age: number | undefined;
    email: string;
  }>();
});

// type-errors/form-invalid-field.ts
// @ts-expect-error - 'phone' doesn't exist in schema
form.setValue('phone', '555-1234');

If you’re building any library with complex types - API clients, query builders, validators - these testing patterns will save you from shipping broken types to your users.

Part 10: Tensor Expressions - Parsing Math at the Type Level

We’ve built two domain-specific languages so far: einsum for index-based tensor operations, and einops for shape transformations. Both use template literal types to parse string patterns at compile time. Now let’s push this further and build a parser for mathematical expressions.

What We’re Building

By the end of this section, we’ll have a system that can take a string like 'a @ b + c' and:

  1. Parse it into a tree structure (called an Abstract Syntax Tree or AST)
  2. Compute the output shape by walking the tree and applying shape rules for each operation
  3. Generate readable errors if shapes don’t match
  4. Compute symbolic derivatives - yes, we can do calculus at the type level!

Here’s what the end result looks like:

const a = torch.randn(2, 3);   // Tensor<[2, 3]>
const b = torch.randn(3, 4);   // Tensor<[3, 4]>
const c = torch.randn(4);      // Tensor<[4]>

// TypeScript parses the expression and computes the output shape
const result = $('a @ b + c')({ a, b, c });
//    ^? Tensor<[2, 4]>  // Computed at compile time!

The $ function (also accessible as torch.tx) uses everything we’ve learned - template literal parsing, type-level arithmetic, and branded error types - to give us type-safe mathematical expressions.

A string expression being fed into a parser machine and producing an abstract syntax tree

Why Parse Expressions?

In machine learning papers, formulas are written mathematically. A simple neural network layer is written as:

y=σ(Wx+b)y = \sigma(Wx + b)

Where σ\sigma is an activation function (like sigmoid), WW is a weight matrix, xx is the input, and bb is a bias. When you implement this in code, it becomes:

// The math: y = σ(Wx + b)
// Method chaining obscures the formula
const y = x.matmul(W).add(b).sigmoid();

The code works, but it’s harder to read than the math. What if we could write code that looks more like the formula?

// This looks more like the math!
const y = $('sigmoid(x @ W + b)')({ x, W, b });

The @ symbol means matrix multiplication (like Python’s @ operator), and the expression reads left-to-right just like the formula.

Step 1: Building an Abstract Syntax Tree

To parse an expression like a @ b + c, we need to understand its structure. This expression means “multiply a and b, then add c”. We can represent this as a tree:

Abstract Syntax Tree for 'a @ b + c' showing (+) at the root with (@) and c as children, and a and b as leaves

This is called an Abstract Syntax Tree (AST). It’s abstract because it captures the meaning of the expression, not the exact characters. The tree structure shows that @ happens first (it’s deeper in the tree), then +.

We can represent this tree as TypeScript types:

// A variable like 'a' or 'b'
type VariableNode<Name extends string> = {
  type: 'variable';
  name: Name;
};

// A number like '42' or '3.14'
type NumberNode<Value extends number> = {
  type: 'number';
  value: Value;
};

// A binary operation like 'a + b' or 'a @ b'
type BinaryOpNode<
  Op extends string,
  Left,
  Right
> = {
  type: 'binary';
  operator: Op;
  left: Left;
  right: Right;
};

With these types, our expression a @ b + c becomes:

type ExprAST = BinaryOpNode<
  '+',                                        // The outer operation is +
  BinaryOpNode<'@', VariableNode<'a'>, VariableNode<'b'>>,  // Left side: a @ b
  VariableNode<'c'>                           // Right side: c
>;

Step 2: Parsing Strings into Trees

Now we need to convert a string like 'a @ b + c' into this tree structure. This is where template literal types come in - we use the same techniques from einsum, but for a more complex grammar.

The key insight is operator precedence. In math, * happens before +. Similarly, @ (matrix multiplication) happens before +. We handle this by parsing in layers:

  1. First, split on + and - (lowest precedence)
  2. Then, split each part on *, /, and @
  3. Finally, handle parentheses and function calls (highest precedence)
// Simplified parsing logic (the real version is more complex)
type ParseExpr<S extends string> =
  // Try to split on '+' first (lowest precedence)
  S extends `${infer Left}+${infer Right}`
    ? BinaryOpNode<'+', ParseExpr<Left>, ParseExpr<Right>>
  // Then try '@' (higher precedence)
  : S extends `${infer Left}@${infer Right}`
    ? BinaryOpNode<'@', ParseExpr<Left>, ParseExpr<Right>>
  // Base case: it's a variable name
  : VariableNode<Trim<S>>;

The actual parser in tx handles many more cases - parentheses, function calls like relu(x), comparison operators, and even ternary conditionals like x > 0 ? x : 0. But the core idea is the same: recursively match patterns and build a tree.

A Simpler Alternative: Reverse Polish Notation

Dealing with operator precedence is complex. There’s a simpler notation that eliminates the problem entirely: Reverse Polish Notation (RPN), also called postfix notation.

In RPN, operators come after their operands instead of between them:

// Infix (what we're used to)
'a @ b + c'     // Need precedence rules: @ before +

// RPN (postfix)
'a b @ c +'     // No ambiguity: read left to right

RPN is unambiguous because you evaluate left to right with a stack:

Tokens flowing through a stack-based evaluator for RPN expressions

  1. See a - push it onto the stack
  2. See b - push it onto the stack
  3. See @ - pop two values, apply @, push result
  4. See c - push it onto the stack
  5. See + - pop two values, apply +, push result

No precedence rules needed! The order is explicit in the notation. torch.js supports RPN via the $.rpn function:

// These are equivalent:
const result1 = $('a @ b + c')({ a, b, c });
const result2 = $.rpn('a b @ c +')({ a, b, c });

// Complex expressions become clearer
// Infix: (a @ b + c) * d
// RPN:   a b @ c + d *
const result3 = $.rpn('a b @ c + d *')({ a, b, c, d });

RPN is popular in calculators (HP calculators famously used it) and stack-based programming languages. For type-level parsing, it’s much simpler to implement since we don’t need the precedence logic.

Beyond tensors: AST parsing isn’t just for math expressions. Every typed DSL you use does this:

// Tailwind: Parses 'bg-blue-500' into structured data
type ParseTailwind<S> = S extends `bg-${infer Color}-${infer Shade}`
  ? { property: 'background'; color: Color; shade: Shade }
  : never;

// Prisma: Parses schema definitions into types
// GraphQL: Parses queries into typed operations
// tRPC: Parses procedure paths into route types
// i18n: Parses translation keys into typed accessors

// The pattern is always the same:
// 1. Parse string into AST (tree structure)
// 2. Walk the tree to compute output types
// 3. Return helpful errors for invalid input

Once you understand AST parsing at the type level, you can build your own type-safe DSLs for any domain - configuration files, query languages, template syntax, or anything else that benefits from compile-time validation.

Step 3: Computing Shapes from the Tree

Once we have an AST, we can walk it to compute the output shape. Each node type has rules:

  • Variable nodes: Look up the shape from the input tensors
  • Binary operations: Apply the operation’s shape rules (matmul, broadcast, etc.)
  • Function calls: Most functions preserve shape (like relu), some change it (like sum)
// Evaluate an AST node to get its shape
type EvalShape<Node, Shapes> =
  // Variable: look up its shape
  Node extends VariableNode<infer Name>
    ? Shapes[Name]
  // Binary op: compute based on operator
  : Node extends BinaryOpNode<infer Op, infer L, infer R>
    ? Op extends '@'
      ? MatmulShape<EvalShape<L, Shapes>, EvalShape<R, Shapes>>
    : Op extends '+' | '-'
      ? BroadcastShape<EvalShape<L, Shapes>, EvalShape<R, Shapes>>
    : never
  : never;

This uses the same MatmulShape and BroadcastShape types we built earlier. The tree structure lets us evaluate complex expressions step by step.

Step 4: Symbolic Differentiation

Here’s where things get interesting. Since we have the expression as a tree, we can apply calculus rules to compute derivatives. This is called symbolic differentiation - we’re manipulating symbols, not numbers.

What is a derivative? If you haven’t taken calculus, here’s the intuition: a derivative tells you how fast something is changing. If f(x)=x2f(x) = x^2, the derivative f′(x)=2xf'(x) = 2x tells you that when x=3x = 3, the function is changing at rate 2×3=62 \times 3 = 6. Derivatives are essential for training neural networks - they tell us how to adjust weights to reduce errors.

A friendly robot wizard applying differentiation rules to transform expressions

The key insight is that differentiation follows simple rules that we can encode as pattern matching:

  • Constants don’t change: The derivative of 55 is 00
  • Variables change at rate 1: The derivative of xx with respect to xx is 11
  • Sum rule: The derivative of a+ba + b is the sum of their derivatives
  • Product rule: The derivative of a×ba \times b is a×b′+a′×ba \times b' + a' \times b
  • Chain rule: For nested functions like sin⁡(x2)\sin(x^2), multiply the outer derivative by the inner derivative

We can implement these rules as a recursive type:

// Compute the derivative of an AST with respect to a variable
type Differentiate<Node, Var extends string> =
  // d/dx(x) = 1
  Node extends VariableNode<Var>
    ? NumberNode<1>
  // d/dx(constant) = 0
  : Node extends NumberNode<any>
    ? NumberNode<0>
  // d/dx(other variable) = 0
  : Node extends VariableNode<any>
    ? NumberNode<0>
  // d/dx(a + b) = d/dx(a) + d/dx(b)  (sum rule)
  : Node extends BinaryOpNode<'+', infer A, infer B>
    ? BinaryOpNode<'+', Differentiate<A, Var>, Differentiate<B, Var>>
  // d/dx(a * b) = a * d/dx(b) + b * d/dx(a)  (product rule)
  : Node extends BinaryOpNode<'*', infer A, infer B>
    ? BinaryOpNode<'+',
        BinaryOpNode<'*', A, Differentiate<B, Var>>,
        BinaryOpNode<'*', B, Differentiate<A, Var>>
      >
  : never;

The actual implementation in tx handles more cases - power rules, trigonometric functions, exponentials, and the chain rule for nested functions. The result is a system that can compute derivatives of complex expressions:

import { $ } from 'torch.js';

// Power rule: d/dx(x²) = 2x
$.grad('x ** 2', 'x')           // '(2 * x ** (2 - 1))'

// Chain rule: d/dx(sin(x²)) = cos(x²) * 2x
$.grad('sin(x ** 2)', 'x')      // 'cos(x ** 2) * (2 * x ** (2 - 1))'

// Neural network activation: d/dx(relu(x)) = 1 if x > 0, else 0
$.grad('relu(x)', 'x')          // 'x > 0 ? 1 : 0'

Practical Applications

This isn’t just an academic exercise. Type-safe expressions are useful for:

  • Catching shape errors early: If you write $('a @ b')({ a, b }) with incompatible shapes, you get a compile-time error
  • Readable code: Mathematical expressions are easier to read than method chains
  • Reusable patterns: Define a pattern once, use it with different tensors
// Define a reusable pattern for a linear layer
const linear = $('relu(x @ w + b)');

// Use it with different tensors - shapes are checked each time
const hidden1 = linear({ x: input, w: weights1, b: bias1 });
const hidden2 = linear({ x: hidden1, w: weights2, b: bias2 });
🚀

Tensor Expressions Lab

Try writing mathematical expressions and see how TypeScript parses them and computes shapes.

Expression Optimizations

A cute optimizer machine simplifying expression trees by removing redundant operations

Since we have the expression as a tree, we can also apply optimizations before evaluating it. The idea is the same as differentiation: walk the tree, pattern match on nodes, and transform them.

For example, to remove identity operations like x+0x + 0 or x×1x \times 1, we pattern match on the AST:

// Optimization rules as tree transformations
type Optimize<Node> =
  // x + 0 -> x (addition identity)
  Node extends BinaryOpNode<'+', infer Left, NumberNode<0>>
    ? Optimize<Left>
  // 0 + x -> x
  : Node extends BinaryOpNode<'+', NumberNode<0>, infer Right>
    ? Optimize<Right>
  // x * 1 -> x (multiplication identity)
  : Node extends BinaryOpNode<'*', infer Left, NumberNode<1>>
    ? Optimize<Left>
  // 1 * x -> x
  : Node extends BinaryOpNode<'*', NumberNode<1>, infer Right>
    ? Optimize<Right>
  // x * 0 -> 0
  : Node extends BinaryOpNode<'*', any, NumberNode<0>>
    ? NumberNode<0>
  // Recursively optimize children
  : Node extends BinaryOpNode<infer Op, infer L, infer R>
    ? BinaryOpNode<Op, Optimize<L>, Optimize<R>>
  : Node;

Each rule matches a pattern and replaces it with a simpler equivalent. The type system does this at compile time, so by the time your code runs, the expression is already simplified.

What about type safety? These optimizations preserve the output shape because they’re algebraically equivalent. x+0x + 0 has the same shape as xx. The type system can verify this: Tensor<[2, 3]> plus a scalar zero is still Tensor<[2, 3]>.

The optimizer handles several categories of simplifications:

  • Identity removal: x+0=xx + 0 = x, x×1=xx \times 1 = x
  • Constant folding: 2+3=52 + 3 = 5 (compute constants at compile time)
  • Inverse pairs: exp⁡(log⁡(x))=x\exp(\log(x)) = x, x2=∣x∣\sqrt{x^2} = |x|
  • Idempotent functions: relu(relu(x))=relu(x)\text{relu}(\text{relu}(x)) = \text{relu}(x)
// See optimizations in action
const expr = $.compileAdvanced('x * 1 + 0');
console.log(expr.getOptimizedExpression());  // 'x'

const expr2 = $.compileAdvanced('exp(log(x))');
console.log(expr2.getOptimizedExpression()); // 'x'

// View what optimizations were applied
console.log(expr.optimizations);
// ['Removed identity: * 1', 'Removed identity: + 0']

These optimizations happen before the expression runs, so there’s no runtime cost for the simplifications. The expression 'x * 1 + 0' becomes just 'x' before any tensor operations occur.

Summary: Three DSLs, One Type System

We’ve now built three domain-specific languages, each with different syntax but all using the same type-level techniques:

DSL
Einsum
Syntax
'ij,jk->ik'
Purpose
Index-based tensor operations
DSL
Einops
Syntax
'b c h w -> b (h w) c'
Purpose
Shape transformations
DSL
tx
Syntax
'relu(x @ w + b)'
Purpose
Mathematical expressions

All three parse strings at compile time, compute shapes, and generate readable errors. The techniques transfer - if you understand how one works, you can build your own DSLs for other domains.

Part 11: Putting It All Together

Let’s recap what we’ve built and how the pieces fit together.

The Architecture

Type-safe tensor operations architecture overview

The Key Patterns

Pattern
Template Literal Parsing
What It Does
Split strings on delimiters
Used In
Einsum, Einops, tx
Pattern
Tuple-Based Arithmetic
What It Does
Add, subtract, compare numbers
Used In
All shape computations
Pattern
Recursive Type Processing
What It Does
Transform arrays element by element
Used In
All parsers
Pattern
Branded Error Types
What It Does
Readable compile-time errors
Used In
All validation
Pattern
Type-Level Key-Value Store
What It Does
Map names to values
Used In
Einsum, Einops, tx
Pattern
Graceful Degradation
What It Does
Fall back for dynamic values
Used In
All types
Pattern
Type-Level Computation
What It Does
Symbolic differentiation, optimization
Used In
tx

Performance: Zero Runtime Cost

All this type-level code completely disappears at runtime. The JavaScript output is just:

const a = torch.zeros(2, 3);
const b = torch.zeros(3, 4);
const c = a.matmul(b);

No type checking at runtime - it all happens during compilation.

When Types Can’t Help

Our types are powerful but have limits:

// Dynamic values aren't checked
const n = parseInt(userInput);
const a = torch.zeros(n, n);  // Tensor<[number, number]> - dynamic
a.at(100);  // Can't check at compile time

We handle this gracefully: when we can’t compute exact types, we fall back to readonly number[].

The Developer Experience

import torch from 'torch.js';

// Create tensors - shapes are inferred
const images = torch.randn(32, 3, 224, 224);      // Tensor<[32, 3, 224, 224]>
const weights = torch.randn(3, 64, 3, 3);         // Tensor<[3, 64, 3, 3]>

// Operations track shapes through einops
const patches = rearrange(images, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', { p1: 16, p2: 16 });
//    ^? Tensor<[32, 196, 768]>

// Slice with full type safety
const firstPatch = patches.at(null, 0);
//    ^? Tensor<[32, 768]>

// Mathematical expressions with tx
const output = $('softmax(x @ w + b, -1)')({ x: patches, w, b });
//    ^? Tensor<[32, 196, vocab_size]>

// Errors caught immediately
const bad = images.matmul(weights);  // Type error!
//    ^? matmul_error_inner_dimensions_do_not_match<224, 3, ...>
🚀

Grand Finale

The ultimate test of torch.js type safety. See all the concepts we've learned - einsum, einops, tx, and shape tracking - combined into one verified flow.

Conclusion

You’ve just learned to program in TypeScript’s type system. Not just “this variable is a string” typing - actual computation: parsing strings, doing arithmetic, building trees, and generating helpful errors. These are the same techniques used by the most sophisticated TypeScript libraries in the ecosystem.

The Techniques You Learned

  1. Template literal parsing: Split strings on delimiters, extract patterns, match syntax
  2. Tuple-based arithmetic: Add, subtract, compare numbers at the type level
  3. Recursive type processing: Transform arrays and strings element by element
  4. Branded error types: Create error messages that explain what went wrong, not just “type mismatch”
  5. Type-level key-value stores: Map names to values for lookup during type computation
  6. Graceful degradation: Fall back to wider types when compile-time checking isn’t possible
  7. Testing type-level code: Verify your types work with assignability checks and expected-error directives

What You Can Build With This

These techniques aren’t just for tensors. You can now build type-safe versions of:

  • API clients: Parse route patterns like /users/:id/posts/:postId and infer parameter types
  • Form libraries: Infer field types from schema definitions, catch invalid field access
  • Query builders: Validate SQL column names against your schema at compile time
  • Configuration parsers: Parse and validate config file syntax in types
  • i18n systems: Type-check translation keys and interpolation parameters
  • CSS-in-JS: Parse and validate style values, catch unit mismatches
  • CLI argument parsers: Infer types from argument definitions
  • State machines: Enforce valid state transitions at compile time

The pattern is always the same: parse a string or structure into an AST, walk it to compute output types, and return helpful errors for invalid input. You now have all the tools to do this.

Go Build Something

The best way to learn is to build. Pick something you work with daily - a REST API, a configuration format, a domain-specific notation - and make it type-safe. Start small: parse one pattern, infer one type. Then add more.

You’ll make mistakes. Types will get confusing. The TypeScript error messages won’t always help. But when you get it working, when your editor catches a bug before you even run the code, you’ll understand why this is worth it.

TypeScript’s type system is a programming language. Now you know how to use it.

Further Reading

← Back to Tutorials